Guess Again Number Sense 7-7 Guess Again Number Sense E7-7

Y'all can read an updated version of this article in our Number Sense and Place Value Feature.

What is number sense?

The term "number sense" is a relatively new one in mathematics education. It is hard to ascertain precisely, but broadly speaking, it refers to "a well organised conceptual framework of number information that enables a person to sympathize numbers and number relationships and to solve mathematical problems that are not leap by traditional algorithms" (Bobis, 1996). The National Quango of Teachers (United states of america, 1989) identified five components that characterise number sense: number significant, number relationships, number magnitude, operations involving numbers and referents for numbers and quantities. These skills are considered important because they contribute to general intuitions about numbers and lay the foundation for more than advanced skills.

Researchers have linked expert number sense with skills observed in students proficient in the following mathematical activities:

• mental calculation (Promise & Sherrill, 1987; Trafton, 1992);
• computational estimation (for case; Bobis, 1991; Case & Sowder, 1990);
• judging the relative magnitude of numbers (Sowder, 1988);
• recognising function-whole relationships and place value concepts (Fischer, 1990; Ross, 1989) and;
• problem solving (Cobb et.al., 1991).

How does number sense begin?

An intuitive sense of number begins at a very early age. Children as young as ii years of age tin can confidently identify 1, two or iii objects before they can really count with understanding (Gelman & Gellistel, 1978). Piaget called this ability to instantaneously recognise the number of objects in a small-scale group 'subitising'. As mental powers develop, usually by about the age of four, groups of four tin be recognised without counting. It is idea that the maximum number for subitising, even for most adults, is five. This skill appears to be based on the mind's ability to grade stable mental images of patterns and associate them with a number. Therefore, it may exist possible to recognise more than 5 objects if they are arranged in a particular style or practice and memorisation takes place. A simple instance of this is half-dozen dots bundled in two rows of three, as on dice or playing cards. Considering this image is familiar, half-dozen tin be instantly recognised when presented this way.

Normally, when presented with more five objects, other mental strategies must exist utilised. For example, we might encounter a grouping of vi objects equally two groups of three. Each grouping of three is instantly recognised, so very quickly (virtually unconsciously) combined to make half dozen. In this strategy no actual counting of objects is involved, but rather a office-part-whole human relationship and rapid mental add-on is used. That is, at that place is an understanding that a number (in this case six) tin be composed of smaller parts, together with the cognition that 'iii plus iii makes six'. This blazon of mathematical thinking has already begun past the fourth dimension children begin schoolhouse and should be nurtured considering information technology lays the foundation for agreement operations and in developing valuable mental calculation strategies.

What pedagogy strategies promote early number sense?

Learning to count with understanding is a crucial number skill, only other skills, such equally perceiving subgroups, demand to develop alongside counting to provide a firm foundation for number sense. Past merely presenting objects (such as stamps on a flashcard) in various arrangements, different mental strategies can exist prompted. For example, showing six stamps in a cluster of four and a pair prompts the combination of 'iv and two makes six'. If the four is not subitised, it may exist seen as '2 and 2 and ii makes 6'. This arrangement is obviously a piffling more than complex than two groups of three. So different arrangements volition prompt different strategies, and these strategies will vary from person to person.

If mental strategies such every bit these are to be encouraged (and simply counting discouraged) then an element of speed is necessary. Seeing the objects for but a few seconds challenges the mind to find strategies other than counting. It is also important to have children reflect on and share their strategies (Presmeg, 1986; Mason, 1992). This is helpful in iii means:

• verbalising a strategy brings the strategy to a conscious level and allows the person to learn about their ain thinking;
• it provides other children with the opportunity to pick upward new strategies;
• the teacher tin appraise the type of thinking being used and arrange the blazon of arrangement, level of difficulty or speed of presentation accordingly.

To begin with, early on number activities are best washed with moveable objects such as counters, blocks and small toys. Most children volition demand the concrete experience of physically manipulating groups of objects into sub-groups and combining small-scale groups to brand a larger grouping. Afterwards these essential experiences more static materials such equally 'dot cards' go very useful.

Dot cards are simply cards with dot stickers of a single colour stuck on one side. (All the same, any markings can be used. Self-inking stamps are fast when making a lot of cards). The important factors in the design of the cards are the number of dots and the arrangement of these dots. The various combinations of these factors determine the mathematical structure of each card, and hence the types of number relations and mental strategies prompted by them.

Consider each of the following arrangements of dots before reading further. What mental strategies are likely to be prompted past each card? What guild would y'all place them in co-ordinate to level of difficulty?

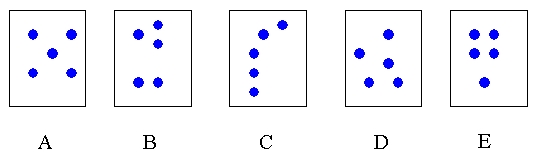
Carte A is the classic symmetrical dice and playing card organization of 5 and and so is often instantly recognised without engaging other mental strategies. It is peradventure the easiest organisation of five to deal with.

Card B presents clear sub-groups of ii and iii, each of which tin be instantly recognised. With practice, the number fact of 'two and iii makes five' tin can be recalled nearly instantly.

Card C: A linear arrangement is the i most likely to prompt counting. However, many people will mentally separate the dots into groups of two and 3, as in the previous card. Other strategies such as seeing ii then counting '3, 4, 5' might also be used.

Card D could be called a random arrangement, though in reality it has been quite deliberately organised to prompt the mental action of sub-grouping. There are a diverseness of ways to class the sub-groups, with no prompt in whatsoever item management, so this card could be considered to be the most difficult one in the gear up.

Card East shows another sub-group organization that encourages the utilize (or discovery) of the 'iv and one makes five' number relation.

Obviously, using fewer than five dots would develop the well-nigh basic number sense skills, and using more than than five dots would provide opportunities for more advanced strategies. Yet, it is probably not useful to apply more than ten dots. (Meet the follow-on article focusing on developing a 'sense of 10' and 'place value readiness'). Cards such as these can be shown briefly to children, so the children asked how many dots they saw. The children should be asked to explain how they perceived the arrangement, and hence what strategies they employed.

What games can assist evolution of early number sense?

Games can be very useful for reinforcing and developing ideas and procedures previously introduced to children. Although a suggested age group is given for each of the following games, information technology is the children'due south level of experience that should determine the suitability of the game. Several sit-in games should be played, until the children become comfortable with the rules and procedures of the games.

Deal and Copy (iv-v years) 3-4 players

Materials: 15 dot cards with a variety of dot patterns representing the numbers from one to five and a plentiful supply of counters or buttons.

Rules: One child deals out one bill of fare face up upwards to each other player. Each child then uses the counters to replicate the arrangement of dots on his/her card and says the number aloud. The dealer checks each result, then deals out a new menu to each actor, placing information technology on tiptop of the previous carte. The children then rearrange their counters to match the new card. This continues until all the cards have been used.

Variations/Extensions

1. Each child can predict aloud whether the new card has more than, less or the same number of dots as the previous card. The prediction is checked by the dealer, past observing whether counters demand to be taken abroad or added.
2. Increment the number of dots on the cards.

Memory Lucifer (5-seven years) 2 players

Materials: 12 dot cards, consisting of vi pairs of cards showing two different arrangements of a item number of dots, from ane to half-dozen dots. (For example, a pair for 5 might be Card A and Carte du jour B from the set above).

Rules: Spread all the cards out face down. The first role player turns over any two cards. If they are a pair (i.e. take the aforementioned number of dots), the player removes the cards and scores a point. If they are not a pair, both cards are turned dorsum downward in their places. The 2d role player then turns over two cards and then on. When all the cards accept been matched, the player with more pairs wins.

Variations/Extensions

1. Increase the number of pairs of cards used.
2. Use a greater number of dots on the cards.
3. Pair a dot card with a numeral card.

What's the Departure? (7-8 years) two-iv players

Materials: A pack of 20 to 30 dot cards (ane to 10 dots in dice and regular patterns), counters.

Rules: Spread out 10 cards face down and place the rest of the cards in a pile face downward. The commencement thespian turns over the top pile bill of fare and places beside the pile. He/she and so turns over one of the spread cards. The player works out the difference between the number of dots on each card, and takes that number of counters. (E.g. If ane card showed three dots and the other 8, the player would take v counters.) The spread card is turned face down again in its place and the adjacent player turns the height pile card so on. Play continues until all the pile cards take been used. The winner is the histrion with the most counters; therefore the strategy is to remember the value of the spread cards so the i that gives the maximum difference can be chosen.

Variations/Extensions

1. Try to turn the spread cards that give the minimum difference, so the winner is the player with the fewest counters.
2. Ringlet a die instead of using pile cards. Offset with a set up number of counters (say twenty), and then that when all the counters have been claimed the game ends.
3. Use dot cards with random arrangements of dots.

The next article in this series is entitled A Sense of 'x' and Place Value.

References

Bobis, J. (1991). The result of instruction on the development of ciphering interpretation strategies. Mathematics Education Research Journal , 3, 7-29.

Bobis, J. (1996). Visualisation and the development of number sense with kindergarten children. In Mulligan, J. & Mitchelmore, M. (Eds.) Children's Number Learning : A Inquiry Monograph of the Mathematics Educational activity Group of Australasia and the Australian Association of Mathematics Teachers. Adelaide: AAMT

Case, R. & Sowder, J. (1990). The development of computational estimation: A neo-Piagetian analysis. Cognition and Education , vii, 79-104.

Cobb, P., Wood, T., Yackel, E., Nicholls, J., Wheatley, G., Trigatti, B., & Perlwitz, M., (1991). Cess of a problem-centred second-grade mathematics project. Journal for Research in Mathematics Education , 22, 3-29.

Fischer, F. (1990). A part-function-whole curriculum for pedagogy number to kindergarten. Journal for Enquiry in Mathematics Education , 21, 207-215.

Gelman, R. & Gallistel, C. (1978). The Child'due south Agreement of Number. Cambridge, MA: Harvard University Press.

Promise, J. & Sherril, J. (1987). Characteristics of unskilled and skilled mental calculators. Periodical for Research in Mathematics Education , 18, 98-111.

Mason, J. (1992). Doing and construing mathematics in screen infinite, In Perry, B., Southwell, B., & Owens, Chiliad. (Eds.). Proceedings of the Thirteenth Annual Briefing of the Mathematics Education Research Group of Australasia . Nepean, Sydney: MERGA.

Ross, S. (1989). Parts, wholes, and place value: A developmental view. Arithmetic Teacher , 36, 47-51.

Sowder, J. (1988). Mental ciphering and number comparison: Their roles in the evolution of number sense and computational estimation. In Heibert & Behr (Eds.). Enquiry Agenda for Mathematics Didactics: Number Concepts and Operations in the Middle Grades (pp. 192-197). Hillsdale, NJ: Lawrence, Erlbaum & Reston.

Presmeg, North. (1986). Visualisation in high school mathematics. For the Learning of Mathematics , 6 (3), 42-46.

Trafton, P. (1992). Using number sense to develop mental computation and computational estimation. In C. Irons (Ed.) Challenging Children to Recall when they Compute . (pp. 78-92). Brisbane: Heart for Mathematics and Science Instruction, Queensland University of Applied science.

flintexciaming.blogspot.com

Source: https://nrich.maths.org/2477

Bagikan Artikel ini